In physical chemistry, Henry’s Law is one of the gas laws. It defines the solubility of a gas within a liquid which is in contact with the same gas above the surface of the liquid. It was formulated in the early 19th century by the English chemist William Henry who described the results of his experiments. In the 21st century, Henry’s Law is the foundation science for multi-billion per year industries, for example the multi-billion dollar per year scientific instruments business of gas chromatography. Henry’s Law also explains why the theory of human-caused global warming /climate change is not even plausible science and should be shunned by knowledgeable people.
Henry’s Law is specifically limited to a phase state equilibrium reaction of a gas and that same gas which is in contact with a liquid solvent, for example CO2 gas in the atmosphere which is in contact with ocean water. Henry’s law only applies to low concentrations of a gas in the mixed gas phase and in the liquid phase. Henry’s Law does not apply to the series of carbonate chemistry reactions occurring in ocean water after the CO2 gas reacts with water and hydrates and disassociates into ions. CO2 gas in atmosphere and in ocean surface satisfies these conditions.
Henry’s Law is dominantly dependent on the temperature at the interface of the gas with the liquid. Rearranging Henry’s Law as d(ln(kH))/d(1/T) defines the temperature dependence parameter in Henry’s Law partition co-efficient, where kH is the Henry’s Law constant and T is temperature in Kelvin. Henry’s Law is explained on the website of the U.S. National Institutes of Standards and Technology. https://webbook.nist.gov/cgi/cbook.cgi?ID=C124389&Units=SI&Mask=10#Solubility
“The chemistry of carbon dioxide is quite complex, but it boils down to reactions as in Eq. (I). In the first step, CO2 of the atmosphere dissolves into the ocean CO2(g)⇌CO2(aq). (I)
In water the CO2 molecules combine with water molecules to form H2CO3 , and this reaction can be written as CO2(aq)+H2O(l )⇌H2CO3(aq). (II)
Here the ratio of the two concentrations of Eq. (I) is given by Henry’s Constant, that depends on the temperature (see Table 6-7 of Lide and Frederikse (1974)), 𝐾h(𝑇)= [CO2(g)] / [CO2(aq)]. (3)” (Stallinga, P. (2018). Carbon Dioxide and Ocean Acidification. European Scientific Journal, ESJ, 14(18), 476. https://doi.org/10.19044/esj.2018.v14n18p476 )
Since the concentration of net global CO2 gas concentration is routinely measured, then Henry’s Law can be used to calculate the concentration of aqueous CO2 gas in ocean surface water.
If net global CO2 concentration in air is 400 ppmv, then, per Henry’s Law KH, at STP, 400 x 10-6 atm. [CO2] = P/KH = 4.00 x 10-4 atm/29.41 atm M-1 = 1.36 x 10-5 M (moles of aqueous CO2 gas per liter of surface ocean water.)
Theoretically, this concentration of aqueous CO2 gas then can be used to roughly calculate the concentration of the carbonates in the series of acid-base reactions in ocean water which occur subsequent to the Henry’s Law phase-state equilibrium reaction, but there are many different equilibrium constants and ocean and atmosphere are very dynamic.
It is incorrect to use average global temperature in Henry’s law calculations, unless that temperature average is weighted by surface area of ocean at a given temperature. However I have not found that information in the scientific literature. Use of global average temperature results in unexplained errors in CO2 concentration. For example, global average ocean temperature is about 17 C, which in the Henry’s coefficient would define ocean as absorbing CO2, which leads to the question: how could global average CO2 concentration be increasing? But the average temperature of the tropical ocean surface is above 26 C year round, which implies tropical ocean surface is emitting CO2 gas year round. The Henry’s Law constant for CO2 and ocean surface water is different at 17 C and 26 C. The Henry’s constant is not constant for different temperatures, which means the ratio of CO2 gas in air versus CO2 gas in ocean water is different at different temperatures. Thus Henry’s Law constants in chemistry text books vary by temperature. A few examples of common errors in the climatology literature are provided below.
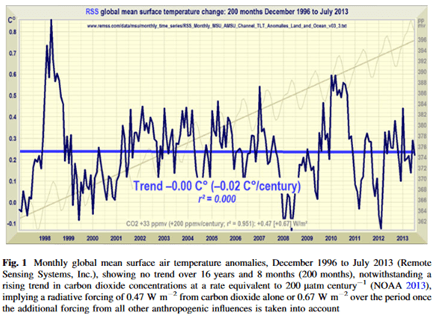
One example is in the following graph, the carefully measured net global CO2 concentration trend (measured at Mauna Loa) versus the RSS satellite-measured global mean surface temperature. The two trends are diverging which by itself immediately falsifies anthropogenic global warming theory. Temperature, density, solubility, pH, specific volume, specific entropy, thermal conductivity, thermal expansion, compressibility are intensive properties in thermodynamics; an intensive property depends only on the type of matter and not on the amount of matter and may vary from place to place within the system at any moment. The average temperature of the earth and the average temperature of earth’s troposphere provide no useful information regarding CO2 flux nor CO2 concentration change nor Henry’s Law and result in errors in calculating CO2 concentration and flux. For example, using Henry’s Law an average ocean temperature of 17 C results in an average global CO2 concentration of about 312 ppmv, which is obviously a large error based on Mauna-Loa-observed net global average CO2 concentration of about 417 ppmv.
Henry’s Law and its partition ratio (co-efficient) for CO2 apply only to this equilibrium reaction: CO2(g)⇌CO2(aq). Henry’s Law does not apply to the hydration reaction of CO2(aq) nor to the several carbonate ion reactions that follow. The ratio of the two concentrations of this first phase state reaction [CO2(g)]⇌[CO2(aq)] is given by the Henry’s co-efficient which depends on temperature (see for example Table 6-7 of Lide and Frederikse (1974), or the Handbook of Chemistry and Physics found in almost all chemistry labs.) In this initial reaction, CO2(g) has not disassociated. Henry’s Law determines the exchange of CO2(g) between the estimated 1000 gigatonnes CO2(g) in ocean surface and the estimated 700 gigatonnes of CO2(g) in the atmosphere; the exchange is estimated as two 90 gigatonnes CO2 per year fluxes in opposite directions, into air and into ocean surface. For comparison humans are estimated to emit into air about 8 gigatonnes of CO2 per year, which is immediately, chaotically mixed with the two 90 gigatonne fluxes into the air and ocean CO2 reservoirs which are both about 10 times larger.
In most climatology literature, aqueous CO2 gas is bundled together and summed with carbonic acid, bicarbonate and carbonate anions in the several initial carbonate chemistry reactions and is usually quantified within the total in millimol/kg-of-solution dissolved inorganic carbon (DIC). Each of these carbon moieties vary based on multiple factors, mainly temperature of the ocean surface, salinity, alkalinity, and CO2 concentration or partial pressure in air immediately above the ocean surface. Consequently, the important Henry’s equilibrium is ignored or confused in usual climate literature resulting in significant, unexplained errors. For example, DIC is directly proportional to CO2(g) ppm in air, but DIC is inversely proportional to ocean surface temperature. If CO2(g) is constant at 400 ppm, then DIC is inversely proportional to ocean temperature while increasing temperature is directly proportional to increasing pH. Clearly it is mistaken to bundle these co-dependent offsetting chemical entities into a single one-dimensional hypothetical reactant. http://www.molecularmodels.eu/Ocean-CO2.pdf
“The analysis of dissolved CO2 in water is an important basis for the assessment of the role of surface waters in the global carbon cycle (Raymond et al., 2013). Indirect methods like calculating CO2 from other parameters like alkalinity and pH (Lewis and Wallace, 1998; Robbins et al., 2010) are affected by considerable random and systematic errors (Golub et al., 2017) caused for example by dissolved organic carbon, which may result in significant overestimation of the CO2 partial pressure (pCO2) (Abril et al., 2015), or by pH measurement errors (Liu et al., 2020). Thus, direct measurement of CO2 is highly recommended, particularly in soft waters.” Koschorreck, M., Prairie, Y. T., Kim, J., and Marcé, R.: Technical note: CO2 is not like CH4 – limits of and corrections to the headspace method to analyse pCO2 in fresh water, Biogeosciences, 18, 1619–1627, https://doi.org/10.5194/bg-18-1619-2021, 2021.
“Measurements of the atmospheric CO2 concentration indicate that it has been increasing at a rate about 50% of that which is expected from all industrial CO2 emissions. The oceans have been considered to be a major sink for CO2. Hence the improved knowledge of the net transport flux across the air–sea interface is important for understanding the fate of this important greenhouse gas emitted into the earth’s atmosphere (1–5).” … “Sources of Errors. The flux estimates are subject to errors from the following five independent sources: (i) the gas transfer coefficients, (ii) the wind speed variability, (iii) the normalization of observations to the reference year of 1990, (iv) the interpolation of limited observations, and (v) skin temperature effect. “The estimated flux values, which range from 0.60 to 1.34 Gt-Czyr21, depend on the choice of sea–air CO2 gas transfer formulations. Hence the error is of a systematic nature and may be reduced if the gas transfer coefficient is better understood in the future.” Taro Takahashi et.al. Global air-sea flux of CO2: An estimate based on measurements of sea–air pCO2 difference. https://www.pnas.org/content/pnas/94/16/8292.full.pdf
While Henry’s law and temperature control the ratio of CO2 in air vs CO2 in ocean surface in the phase state reaction CO2(g)⇌CO2(aq), the enormous excess of aqueous CO2(g) in ocean is controlling the stoichiometry of the acid-base carbonate chemistry. The activities of carbonic acid, bicarbonate and other intermediate carbonate ions are constrained, being suppressed by the 1000 times excess of calcium ions and silicon ions with respect to carbonate ions as well as alkalinity in the ocean buffering systems. Segalstad, Stumm and Morgan and others have pointed out that ocean water is an infinite sink, an infinite buffer for CO2; In the hydration reaction CO2(g) + H2O(l) ⇌ H2CO3(aq), carbonic acid ( H2CO3), the weak acid created by hydrating CO2, can never make ocean acidic.
The alkaline ocean and buffers for carbonate ions allow seawater to dissolve and react with huge amounts of aqueous CO2 gas. Once hydrated into carbonic acid, the phase state reaction CO2(g)⇌CO2(aq) is unbalanced, which causes absorption of additional CO2 gas from atmosphere into the ocean surface. To calculate the true equilibrium value of CO2 gas in the air and aqueous CO2 in ocean surface, all stoichiometry mass balances and kinetics of all of the carbonate chemical reactions must be simultaneously computed, accounting for the equilibrium constant of each reaction, and each of these reactions in turn depend on temperature, alkalinity, and salinity. These are complicated simultaneous differential equations.
In ocean water, CO2 molecules hydrate in seconds to form H2CO3, but this does not mean the CO2(g)⇌CO2(aq) phase state equilibrium can be ignored as usually done in climatology literature. Evidence of over 1000 gigatonnes of aqueous CO2 gas in ocean surface cannot be ignored. Also the hydration reaction aqueous CO2(g) + H2O(l) ⇌ H2CO3(aq) is more complicated than it is usually represented in climatology literature. Combining the CO2(g)⇌CO2(aq) phase state reaction controlled by Henry’s Law solubility with the CO2(g) + H2O(l) ⇌ H2CO3(aq) hydration reaction and calling it simply HCO3* or H2CO3*, which are non-existing hypothetical entities, leads to stoichiometric errors in the various carbonate chemistry reactions as well as in the CO2(g)⇌CO2(aq) phase state equilibrium reaction. The errors and uncertainty are often larger than the CO2 emission flux attributed to humans. For example in “Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: validation based on laboratory measurements of CO2 in gas and seawater at equilibrium” by Timothy J Lueker Andrew G Dickson Charles D Keeling. https://www.sciencedirect.com/science/article/abs/pii/S0304420300000220. or https://doi.org/10.1016/S0304-4203(00)00022-0 The kinetics and stoichiometry of hydration and the chemistry and kinetics of CO2(g)⇌CO2(aq) phase state reaction are omitted entirely.
The hydration equilibrium constant at 25°C is Kh, which in the case of carbonic acid is [H2CO3]/[CO2] ≈ 1.2×10−3 in seawater. Hence, the majority of the carbon dioxide in sea water is not converted into carbonic acid; it remains as aqueous CO2 molecules. Alan L. Soli, Robert H. Byrne, CO2 system hydration and dehydration kinetics and the equilibrium CO2/H2CO3 ratio in aqueous NaCl solution, Marine Chemistry, Volume 78, Issues 2–3, 2002, Pages 65-73, ISSN 0304-4203, https://doi.org/10.1016/S0304-4203(02)00010-5. https://www.sciencedirect.com/science/article/pii/S0304420302000105
Source: Stumm and Morgan. Aquatic Chemistry. Page 210.
This short video explains the Henry’s Law equilibrium equation. Note also the professor’s comment about ammonia being “scrubbed” by water since CO2 is “scrubbed” from the air by water in ocean surface in the same manner. https://archive.org/details/ucberkeley_webcast_-ziliLAdom4
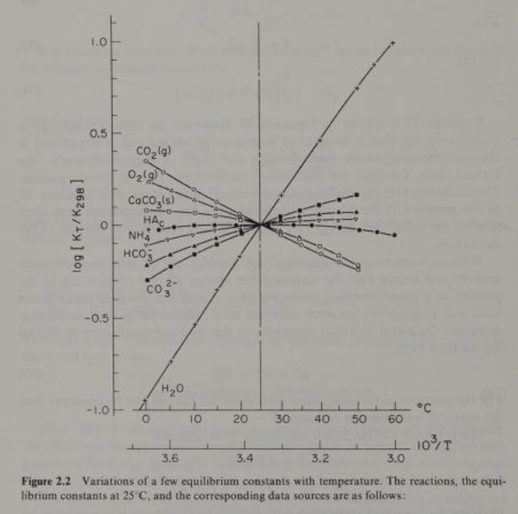
As already mentioned, the Henry’s equilibrium “constant” or co-efficient for CO2(g) is not constant with respect to temperature. Also, the equilibrium “constants” for 3 other reactants and products in the initial carbonate chemistry series are not “constant” with respect to temperature. Figure 2.2 above from Morel illustrates significant variation in the equilibrium constants with respect to standard temperature (25 C). Clearly, bundling these offsetting widely varying reactants and products together in a bundled hypothetical reaction will lead to errors.
“The Henry’s constant typically increases with temperature at low temperatures, reaches a maximum, and then decreases at higher temperatures. The temperature at which the maximum occurs depends on the specific solute-solvent pair.”…”It is important to recognize that the Henry’s “constant” is a strong, nonlinear function of temperature. For accurate design, it is preferable to have temperature-dependent data for Hi(T).”.. Additional pitfalls include failing to distinguish between the “solubility” and the “volatility” form of Henry’s law, failing to consider the implications of liquid-phase solute partitioning, and failing to be careful about units of measure, especially dimensionless units.” Harvey, A. and Smith, F. (2007), Avoid Common Pitfalls when using Henry’s Law, Chemical Engineering Progress, [online], https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=50449 (Accessed August 14, 2021).
Example papers of observed temperature-dependent CO2 emission or absorption or fugacity from ocean surface:
“Based on these observations, 72% of the increase in fCO2sea in Cariaco Basin between 1996 and 2008 can be attributed to an increasing temperature trend of surface waters, making this the primary factor controlling fugacity at this location.” Astor, Y. M.; Lorenzoni, Laura; Thunell, R.; Varela, R.; Muller-Karger, Frank E.; Troccoli, L.; Taylor, G. T.; Scranton, M. I.; Tappa, E.; and Rueda, Digna, “Interannual Variability in Sea Surface Temperature and Fco2 Changes in the Cariaco Basin” (2013). Marine Science Faculty Publications. 1057.
https://scholarcommons.usf.edu/msc_facpub/1057 . https://doi.org/10.1016/j.dsr2.2013.01.002
Note that the discussion and interpretations in the above paper attempt to support AGW. But the data in the paper support the case which is presented here. There are many papers like this from geographies around the world.
“Small changes in the largest marine carbon pool, the dissolved inorganic carbon pool, can have a profound impact on the carbon dioxide (CO2) flux between the ocean and the atmosphere, and the feedback of this flux to climate.” Irina I. Pipko, et.al. The spatial and interannual dynamics of the surface water carbonate system and air–sea CO2 fluxes in the outer shelf and slope of the Eurasian Arctic Ocean. Ocean Sci., 13, 997–1016, 2017
https://doi.org/10.5194/os-13-997-2017
“On the one hand, the hypothesis of Henry’s Law tells us that CO2 variations in the atmosphere are the result of temperature changes. We had already shown that for historical long-term data Henry’s Law is correct [ 12 23 ], as well as for periodic data of a specific meteorological station, De Bilt (Netherlands) [ 17 ].” … “Analyzing the contemporary data of Figure 3, we can conclude that Henry’s Law can readily explain this: every time warm water appears at the surface of the oceans, a huge amount of CO2 is released into the atmosphere (or less is absorbed than could be absorbed by cold waters), and in La Niña years when cold water reaches the surface, more CO2 is taken back to the oceans. It is even consistent with the value obtained on basis of thousands-of-years historical data (10 ppm/K [ 12 ]).” Analysis of Temporal Signals of Climate. Peter Stallinga, Igor Khmelinskii. FCT and CEOT, University of the Algarve, Faro, Portugal. https://DOI.org/10.4236/ns.2018.1010037 . https://www.scirp.org/pdf/NS_2018101510264849.pdf
“The biogeochemical cycling of carbon between its sources and sinks determines the rate of increase in atmospheric CO2 concentrations. The observed increase in atmospheric CO2 content is less than the estimated release from fossil fuel consumption and deforestation. This discrepancy can be explained by interactions between the atmosphere and other global carbon reservoirs such as the oceans, and the terrestrial biosphere including soils. Undoubtedly, the oceans have been the most important sinks for CO2 produced by man.” … “The instability of current models to estimate accurately oceanic uptake of CO2 creates one of the key uncertainties in predictions of atmospheric CO2 increases and climate responses over the next 100 to 200 years.” Peng, T H, Post, W M, DeAngelis, D L, Dale, V H, and Farrell, M P. Atmospheric carbon dioxide and the global carbon cycle: The key uncertainties. United States: N. p., 1987. Web. ACS Publications.
Note that the discussion and interpretations in the paper immediately above attempt to support AGW. But the data in the paper support instead the case which is presented here. There are many papers like this from all around the world.
“There is a decline, or a negative trend, in the air-sea pCO2 gradient of 23 μatm over the decade, which can be explained by a cooling of 1.3 °C over the same period.” Shadwick, E. H. et al., Air-Sea CO2 fluxes on the Scotian Shelf: seasonal to multi-annual variability. Biogeosciences, Volume 7, Issue 11, 2010, pp.3851-3867. November 2010. https://DOI.org/10.5194/bg-7-3851-2010. https://bg.copernicus.org/articles/7/3851/2010/bg-7-3851-2010.pdf
The rate limiting step for re-equilibrating the partial pressure of aqueous CO2 gas in ocean surface is the migration time for CO2 gas in the ocean surface water. This is both vertical and horizontal migration and there are many variables. There are 2 thin layers at the gas – liquid ocean surface which slightly delay emission of CO2 gas from ocean surface into air. But this delay is not the rate limiting step for the emission flux. These thin films involve simultaneous virial kinetics, Van der Waals forces and surface tension.
Changes in atmospheric CO2 concentration are observed to lag (occur after) variations in earth’s surface temperature by 6 to 9 months and longer. The papers by Stallinga and Khmelinskii above discuss this in detail using the example of Pinatubo volcano eruption in 1991, which, after the volcano injection of CO2, the net global CO2 concentration returns to the long term trend in rate of change of CO2 concentration in air with respect to time (dCO2/dt), recorded at Mauna Loa, and then returns to the Henry’s partition ratio which existed prior to the perturbation in ocean surface temperature which was caused by the global belt of high altitude clouds and ash which cooled ocean surface around the equator; no permanent or long term offset of CO2 concentration or slope is observed.
“It is critical to note that the sea must heat before the level of atmospheric CO2 can rise – not the other way around. This is important because it proves that increasing levels of anthropogenic produced CO2 cannot cause the sea to heat initially – whether that additional CO2 causes the global surface temperatures to rise or not. Satellite records shows there is a recorded increase in sea surface temperatures over recent years which basic science, shows must be causative of increased levels of CO2 in the atmosphere. CO2 is a heavy gas (1.5 times air) and remains in close contact with the sea surface. This permits rapid stoichiometric balancing of sea and atmospheric CO2 during season changes.” https://bosmin.com/SeaChange.pdf
“The rate of mass transfer from pure CO2 effluent discharged in the deep ocean depends strongly on the solubility of CO2 in seawater. This thermodynamic study derives solubility relationships for both gas- and liquid-phase CO2 in seawater. It is determined that, for CO2 gas, solubility depends on both temperature and pressure and, as a consequence, solubility increases sharply with depth in the ocean.” H.Teng1S.M.Masutani1 C.M.Kinoshita1 G.C.Nihous2, Solubility of CO2 in the ocean and its effect on CO2. https://doi.org/10.1016/0196-8904(95)00294-4
When ocean surface exceeds 25.6 C it out-gases CO2 gas into the air from ocean surface. In another location, ocean surface which is less than 25.6 C will absorb CO2 gas into the ocean surface. Both CO2 absorption and emission are almost immediate if the aqueous CO2 gas is present at the ocean surface. If the ocean surface has been warm, windy or turbulent for an extended time period, then the partial pressure aqueous CO2 gas in the ocean surface will be lower, that is under-saturated with CO2 with respect to the Henry’s ratio for that temperature. Depletion of the aqueous CO2 gas from the local surface area requires time to recover to saturation due to the resistance to migration of the CO2 in the ocean water matrix.
“Here we use global-scale atmospheric CO2 measurements, CO2 emission inventories and their full range of uncertainties to calculate changes in global CO2 sources and sinks during the past 50 years. Our mass balance analysis shows that net global carbon uptake has increased significantly by about 0.05 billion tonnes of carbon per year and that global carbon uptake doubled, from 2.4+/-0.8 to 5.0+/-0.9 billion tonnes per year, between 1960 and 2010.” https://cfc.umt.edu/research/gcel/files/Ballantyne_IncreasedCO2Uptake_Nature_2012.pdf
In other words, globally averaged, CO2 concentration in air is increasing and CO2 gas concentration in ocean surface is also increasing. The Henry’s partition ratio is re-equilibrating to a larger area of ocean surface area which is above 25.6 C.
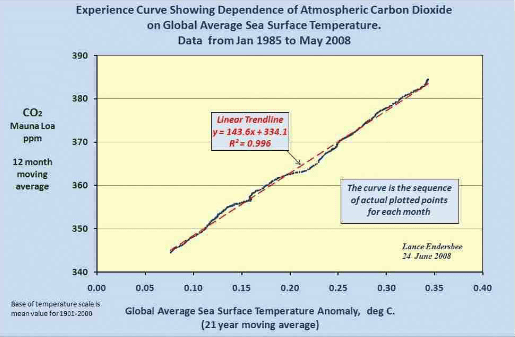
The late professor Lance Endersbee demonstrated that a straight line relationship exists with near perfect correlation between sea temperature with respect to CO2 concentration, consistent with Henry’s Law when time is de-seasonalized. http://icecap.us/images/uploads/Focus_0808_endersbee.pdf
In conclusion, science observations and theory confirm that the atmospheric level of CO2 is always in balance with the sea surface temperature or else is dynamically moving through very large fluxes to re-establish that balance. In one geography, CO2 gas is being absorbed into ocean surface while in another location CO2 is being emitted into air from the ocean surface. The amount of CO2 gas emitted into air by humans (about 8 gigatonns per year) is trivially small with respect to both the existing CO2 reservoir in air (about 700 gigatonnes) and the existing CO2 reservoir in ocean surface (about 1000 gigatonnes) and it is also trivially small with respect to the two ongoing annual fluxes of CO2 (about 90 gigatonnes each) circulating between the atmospheric CO2 reservoir and ocean surface reservoir. The human emission is easily absorbed by ocean surface. But the critically important point is that the source of the CO2 is not a variable in Henry’s law equilibrium reaction. Atmospheric CO2 concentration is not affected by humans but instead is controlled by natural chemical and physical processes which control CO2 solubility in ocean water. Similarly, CO2 residence time in atmospheric is also irrelevant to this chemistry and physics. CO2 gas will always find the equilibrium concentration ratio between sea surface and air determined by Henry’s Law which is a function of sea surface temperature at that location. Globally averaged, the other variables which are functions in Henry’s Law cancel out, i.e., salinity, alkalinity, surface winds, water surface turbulence, and pressure cancel out globally, though they do have effect locally.
Hermann Harde. What Humans Contribute to Atmospheric CO2: Comparison of Carbon Cycle Models with Observations. Earth Sciences. Vol. 8, No. 3, 2019, pp. 139-159. https://doi.org/10.11648/j.earth.20190803.13
M. L. Salby, “Atmospheric Carbon”, Video Presentation, July 18, 2016. University College London. https://youtu.be/3q-M_uYkpT0.
M. L. Salby, “What is Really Behind the Increase of Atmospheric CO2“? Helmut-Schmidt-University Hamburg, 10. October 2018, https://youtu.be/rohF6K2avtY
M. L. Salby, “Relationship Between Greenhouse Gases and Global Temperature”, Video Presentation, April 18, 2013. Helmut-Schmidt-University Hamburg https://www.youtube.com/watch?v=2ROw_cDKwc0.
E. Berry, “Human CO2 has little effect on atmospheric CO2“, 2019. https://edberry.com/blog/climate-physics/agw-hypothesis/contradictions-to-ipccs-climate-change-theory/
Stallinga, P. (2020) Comprehensive Analytical Study of the Greenhouse Effect of the Atmosphere. Atmospheric and Climate Sciences, 10, 40-80. Full paper in pdf here: https://www.scirp.org/pdf/acs_2020011611163731.pdf
Analysis of Temporal Signals of Climate. Peter Stallinga, Igor Khmelinskii. FCT and CEOT, University of the Algarve, Faro, Portugal. https://DOI.org/10.4236/ns.2018.1010037
budbromley 
Bob C’s proof that ACO2 does not cause all or even most of the increase in CO2:
We know from empirical data (the bomb spike) that atmospheric concentrations decay back to equilibrium in an exponential curve, C(t) = C(t=0)exp(-t/a), where a is the time constant of the decay (and ~0.7a is the half-life).The decay rate at any time, t, is dC/dt = -1/a * C(t=0)exp(-t/a) = -1/a * C.
Hence, the concentration decay rate is proportional to the concentration (what makes the system linear, and is the generating definition of an exponential). (we refer to all rates and quantities as positive, and identify which way they’re going by labelling “in” -to the atmosphere, and “out” -of the atmosphere.).
Let’s suppose we have an equilibrium with Rin = Rout, and C = constant. If we measure Rin = Rout = 100Gt/yr (carbon, not CO2), and C = 800Gt, we can immediately deduce the time constant, since R = 1/a * C, we get a = C/R = 8 years. (This is ~ 30% smaller than derived from the bomb spike data, so perhaps there is more than 800Gt C in the atmosphere, or we need to include some fraction of the biosphere, or the estimates of Rin, Rout are high.).
Now, let’s suppose we add an Anthropogenic component, “Ain”, to “Rin”, and continue doing so for an indefinite time. How much does C increase? There are two ways of doing this – both easy since the system has been measured to be (nearly) linear:
1) Increase at equilibrium (t -> infinity):Since Rin = 1/a*C_natural, then (Rin + Ain) = 1/a * (C_natural + C_anthro). These linear equations are easily solved for C_anthro = a * Ain. Hence, if Ain = 8Gt/year, C_anthro = 64Gt/year, or about 8% of total atmospheric concentrations. (Also, about 30 ppm). Note that this is the maximum concentration increase that can be caused by an Anthropogenic input of 8 Gt/yr that continues forever. It does not continue to build up, because that assumption is equivalent to assuming that the time constant, “a”, is very large – 100’s of years. Making this (hidden) assumption then raises the problem of where is all the missing carbon in the atmosphere (or equivalently, why is the carbon cycle so very far out of balance?) Also, of course, such an assumption cannot explain the bomb spike data without ad hoc assumptions about the behaviour of C14 vs C12.
2) The same result can be gotten by considering the discrete yearly increases in C anthro: Year 1 total C_anthro = AinYear 2 total C_anthro = Ain + (1-1/a)AinYear 3 total C_anthro = Ain + (1-1/a)Ain + (1-1/a)^2 * Ain…Year n total: C_anthro = Ain * Sum(r^n), where n goes from 0 -> n , (r=1-1/a) This is a geometric series, whose partial sum (at year N) is: C_antho = Ain *(1-r^n)/(1-r),and the infinite sum (at forever) is: C_anthro = Ain *1/(1-r) = a*Ain (after substituting r = 1-1/a).
So to summarize:1) Measurements show that the atmosphere adjusts to an input of CO2 by an exponential decay. This implies that the sink rates are proportional to the concentrations. 2) Both the measurements and estimates from total CO2 amounts give similar time constants for the decay. 3) Points 1 and 2 put a limit on the increase in CO2 atmospheric concentration that can be caused by a continuous anthropogenic input to the yearly input times the time constant. 4) The claim that a continuous anthropogenic input can cause a continuous, fixed increase in CO2 atmospheric concentration contradicts both the measurements in point 1 and the estimates in point 2, hence is false.
LikeLike
Cohenite,
Was indeed a lot of comment at that time!
When rereading my comments, I saw that I made one mistake: the 14CO2 decay rate is much faster than for for 12CO2, not because there is less mass of it, but because far less returns back to the atmosphere than for 12CO2. But that is for later. Now about Bob C’s “proof”…
It starts good: the formula for the decay rate of 14CO2 back to equilibrium is right.
Next alinea it gets wrong: “the concentration decay rate is proportional to the concentration” which is not the case, as that implies that CO2 could drop to zero as “equilibrium”. The concentration decay rate is proportional to the concentration above the real equilibrium, not zero. For the current average ocean surface temperature the equilibrium is 295 ppmv, thus any level above 295 ppmv will give an extra output, proportional to that extra level.
Then the next point: what he uses in the calculation for the time constant is NOT the decay rate, that is the definition of the residence time, nothing to do with the decay rate of an excess amount of CO2 above equilibrium.
The formula for the residence time is total mass / throughput, where throughput = input = output when everything is in equilibrium. No matter the direction of the throughput. In the case of natural CO2 the throughput is mostly seasonal: from the oceans to vegetation in spring/summer and from vegetation to the oceans in fall/winter. As those fluxes are estimated around 210 GtC/year, partly diuranal (vegetation), partly seasonal, that gives a residence time of 800 GtC / 210 GtC/year = less than 4 years. Be aware: all these flows are bidirectional and don’t change the total amount in the atmosphere at the end of the year when in equilibrium. There is however a small seasonal amplitude of about 9 GtC, as the biosphere fluxes are larger than the ocean fluxes in countercurrent of each other.
Thus Bob C did use the wrong formula, the one for the residence time which is not applicable here, as when one flux removes CO2 as result of seasonal temperature changes, another flux adds CO2 at the same time as result of temperature changes and both are prsctically independent of the amounts already in the atmosphere, thus near independent of the CO2 pressure.
Then what is the real e-fold decay rate?
If you add some extra CO2 in the atmosphere, the partial pressure (pCO2) of CO2 increases and the input flux of CO2 from the oceans in spring/summer will drop a little while the output flux into the oceans in fall/winter will increase a little. It is that difference that gives the real decay rate, as that is proportional to the increase of CO2 above the current equilibrium of 295 ppmv. Not the total or the height of the fluxes, but the difference in inputs and outputs and that is about 2%/year of the extra pressure in the atmosphere above equilibrium or an e-fold decay rate of around 50 years.
About the difference between the excess 14CO2 decay and the excess 12CO2 decay: both have about the same speed of absorption, depending of the excess level above equilibrium for each of them on its own. The 14CO2 peak spreaded from the atmosphere over the ocean surface and vegetation and in 1960 all three reservoirs had their maximum 14CO2 level from the bomb tests, more or less in equilibium with each other. The difference is in the deep oceans: what did go into the deep oceans was the extra level of 1960, but what did come out was the level of some thousand years before, long before any human intervention. That makes that for 1960, some 97.5% of 12CO2 mass returned in the same year as dissolved in the deep oceans, but only 45% of 14CO2. That is the cause of the much faster 14CO2 decline than for an 12CO2 decline after an extra supply above equilibrium. See: http://www.ferdinand-engelbeen.be/klimaat/klim_img/14co2_distri_1960.jpg
Ferdinand
LikeLike
“Next alinea it gets wrong: “the concentration decay rate is proportional to the concentration” which is not the case, as that implies that CO2 could drop to zero as “equilibrium”. The concentration decay rate is proportional to the concentration above the real equilibrium, not zero. For the current average ocean surface temperature the equilibrium is 295 ppmv, thus any level above 295 ppmv will give an extra output, proportional to that extra level.”
I think you have misinterpreted BobC. Bob and I wrote about th is some time ago in the context of the dispute between Essenhigh and Cawley:
https://australianclimatesceptics.com/?p=1
To summarise: Cawley asserts that the “one-box model of the carbon cycle used in ES09 [Essenhigh] directly gives rise to (i) a short residence time of ~4 years, (ii) a long adjustment time of ~74 years”.
Effectively, this means that while one ACO2 molecule does not remain long [4 years] the effect of all the ACO2 on the atmospheric bulk is long-lasting [74 years] and therefore supports the idea that ACO2 is the main reason for the increase in CO2.
However, Essenhigh uses a “one box” model in which flux from the atmosphere has a proportional relationship with the concentration [bulk] of CO2. Essenhigh expresses this as:
F=k*C, where F is the flux from the atmosphere to the environment, C is the atmospheric concentration, and k is a proportionality constant.
Cawley changes this to F=k*C +F0, where F0 is a constant flux independent of atmospheric concentration.
This assumption by Cawley contradicts Henry’s Law. Henry’s Law says that the rate of diffusion or movement of gas from the atmosphere is dependent on temperature and the concentration of the gas; as the concentration changes so does the rate of movement. But Cawley’s constant, F0, would mean that when there is zero CO2 in the atmosphere (C=0) there would still be a finite flux (F0) of CO2 from the atmosphere! That is to say Cawley’s model allows for bulk CO2 to become negative.
LikeLike
About point 2) from Bob C:
Proven false, as the current amount of fossil CO2 in the atmosphere is already around 10% with a maximum of 5% of all influxes. Just the result of taking the residence time and not the real decay rate…
LikeLike
Ferdi, the only thing proven false is your statement there. The percentage of human CO2 in the atmosphere has no effect on the climate. You don’t understand Henry’s Law and Le Chatelier’s principle. CO2 residence time is irrelevant, a distraction. The molecule of CO2 emitted into air is not the same molecule that is absorbed elsewhere by ocean, land and biosphere. The emitted CO2 molecule temporarily increases the partial pressure of CO2, a partial pressure which is re-balanced elsewhere by any CO2 molecule being absorbed.
LikeLike
Bud,
I didn’t use the residence time at all, but Bob C used it to calculate the decay rate for an extra shot CO2 above equilibrium (in the case of Bob C down to zero CO2, another error). I do agree that that CO2 has little effect on climate, but you underestimate the time it needs to remove any extra CO2 above the equilibrium: that is about 50 years e-fold time or 37 year half life time. Not less than a year as you think.
It is not because a lot of natural CO2 is moving back and forth between oceans and vegetation, that with 1 % more CO2 in the atmosphere suddenly 1% more leaves are growing on the trees or that the ocean surface suddenly absorbs 1% more CO2… That takes more time to react…
Further, in the case of Henry’s law, that counts only for pure, dissolved CO2, not for bicarbonates and carbonates. CO2 + bicarbonates + carbonates form together DIC (dissolved inorganic carbon) in the ocean surface that can go back and forth between the three, depending of pH, salt content, CO2 pressure in the atmosphere,…
In fresh water CO2 is 99%, bicarbonate 1% carbonate 0% In seawater CO2 is 1%, bicarbonate 90%, carbonate 9%
If the CO2 pressure in the atmosphere doubles, then pure CO2 doubles in fresh water, still over 99%. In seawater it goes only from 1% to 2% (thus obeying Henry’s law) and lowers the % of the others, while increasing them in mass too, but not more than with some 10% for total DIC, not 100%. That is the Revelle/buffer factor. Still the total carbon dissolved in seawater for a doubling of CO2 in the atmosphere is 10 times higher than in fresh water… See the Bjerrum plot for the difference in % species (not the total dissolved!) in water at different pH levels: https://en.wikipedia.org/wiki/Bjerrum_plot
LikeLike
Ferd, the entire argument about carbon isotope ratio and claiming 10% of atmospheric CO2 is human-emitted is the residence time argument. A total distraction.
The capacity of the environment to both absorb and emit CO2 within a year greatly exceeds human emission within a year. This large excess in natural capacity is observed by measuring the annual cyclical saw tooth emission and absorption (due of photosynthesis differences), as I have already explained to you several times.
Why don’t you go back and read my article on Henry’s Law before commenting? I explained Henry’s Law only applies to the equilibrium reaction where CO2 gas has a phase state reversible reaction to aqueous CO2 gas. It does not apply to the carbonate chemistry, as I explained in detail with references.
Ocean is 98% of the water on the planet and >70% of earth’s surface. Your fresh water argument is nonsense. Pointless. Your argument about trees is equally pointless. CO2 has been increasing about 2.5 ppmv per year, and that is a very good thing for trees and everything else on the planet, but human contributed CO2 is not involved. More CO2 would be much better. But the human contribution is zero. CO2 concentration in air and ocean surface is the same as it would be if humans never existed. Henry’s Law (the ratio of aqueous CO2 gas in ocean surface versus CO2 gas above ocean surface) is independent of the source of the CO2. The Henry’s ratio is a non-linear function of ocean surface temperature.
LikeLike
Ferdi, I will not publish your last few comments on my blog. You cannot publish false information here. I have replied previously to each of your points. Yet you repeat the same points. It is incorrect to use average global temperature in Henry’s Law calculations. Thus, calculations of a global CO2 equilibrium concentration are wrong. Atmospheric fraction of human CO2 is a distraction, useless and misleading. The Henry’s Law coefficient and CO2 partition ratio are functions dominantly of surface temperature, but not average surface temperature. The Henry’s coefficient is independent of the source of the CO2. For any amount of human CO2 emission, there is an equal amount of CO2 absorbed by the environment, primarily ocean surface. Human emission is an insignificant perturbation which is rebalanced to the partition ratio for the local conditions, primarily surface temperature, although alkalinity, salinity and air and water disturbances also affect local conditions. Take your mistaken and false notions to one of the many leftist, global resetter blogs, social media and news outlets.
LikeLiked by 1 person
Knoor finds a constant airborne fraction (AF) for the last 150 years:
Click to access knorr2009_co2_sequestration.pdf
The AF is the % of ACO2 emissions which remain in the atmosphere contributing to the increase in atmospheric CO2 levels. If the ACO2 AF is constant that must mean non-ACO2 or natural emissions of CO2 are contributing to the increase in the bulk CO2 concentration.
The reason for this is the principle of a constant in an increasing total: say ACO2 is 20% of all CO2 which is 100, so ACO2 is 20 and natural CO2 is 80; when all CO2 is 200 ACO2′s 20% will be 40 so natural CO2 will be 160, an increase of 80; at 300, ACO2 is 60, natural CO2 is 240 and so on; natural CO2 must be contributing to the increase in total CO2.
Knoor has been supported by the Gloor et al paper.
https://acp.copernicus.org/articles/10/7739/2010/acp-10-7739-2010-discussion.html
LikeLike
Ferdinand, use of long term proxy data from ice cores is not useful and subject to many errors as many scientists have explained. You can cite all the proxy papers you want, but they do not explain the current observed empirical evidence such as dCO2 following dSST. For your theory to be plausible, dCO2 must precede dSST. dCO2 preceding dSST would directly contradict Henry’s Law which has been used daily for over 100 years by thousands of chemists. Try your thoughts in calculations in the Chemistry Work Bench online. Occam’s razor. Ocean surface contains a huge amount of CO2 gas. Ocean surface has been in a warming trend on average since the last ice age. The trend of warming ocean surface produces a trend of increasing CO2. It is not complicated. Ancient ice cores are not needed nor useful for contemporary estimates.
LikeLike
Bud, ice core CO2 measurements are as accurate as direct measurements in the atmosphere and are made with the same equipment…
The only drawback is that these are averages over less than ten (Law Dome) to 600 years (Vostok). Even so, the Vostok ice core shows that natural CO2 changes follows temperature changes with 800 +/- 600 years during warming and with several thousands of year during cooling.
That also is the case for fast temperature changes: seasonal (opposite: temperature increases, CO2 drops) and year by year (El Niño, Pinatubo: positive with temperature).
But the sudden increase of CO2 since 1850 is NOT caused by temperature, that simply violates Henry’s law,. which gives not more than 12-16 ppmv/K for current ocean surface temperatures.
Quantities of CO2 dissolved in the oceans and atmosphere don’t play any direct role in the equations, as only the CO2 pressure (pCO2) difference between ocean surface and atmosphere gives a transfer between these two.
It doesn’t make much difference for the pressure under the screw cap if you shake a bottle of Coke filled from the same batch if that is 0.5, 1.0 or 1.5 liter, that will be the same (except for a relative larger loss out of the liquid in the smallest bottle).
BTW, by taking the derivatives, you remove most of the trends and let it be the trends where human emissions are twice the increase in the atmosphere. That is the carbon mass balance…
dSS only modifies the net sink rate of oceans and vegetation (not the source rate, as nature is more sink than source!) which results in only +/- 1.5 ppmv variability around the 90+ ppmv trend in the past 60+ years, caused by 180+ ppmv emissions from humans…
LikeLike
Ferdinand, I like your analytical mind as expressed in your comments here as well as your intense discussions over at WUWT. Let me suggest that you go back to first principles and re-calculate. All of the variables, known and unknown, in discussions and papers with regard to local ocean temp, pCO2, pH, insolation, salinity, slope, etc also apply to air trapped in ice thousands and millions of years ago, and then several more variables must be added such as compression of the air bubbles, melt rates, etc. which do not affect a CO2 concentration measurement (for example Mauna Loa) today. Ice cores should not be used as proxy for global conditions. Salby explains some of the error in one of his videos where Harde introduces Salby so I think it is one of his lectures from Germany or Netherlands.
LikeLike
Bud, I have followed one of the lectures of Dr. Salby in the London’s Parliament several years ago. Unfortunately, there was no time for a full discussion of even the most important items of disagreement. And he never discusses things out, ever. Which is a very weak point.
One of the other points where he was wrong was… ice cores. According to him there must be a lot of migration over time. Which is impossible, as if that was the case, for each interglacial back in time, the original CO2 must have been higher and higher to give the same result as measured today, which implies a negative original CO2 level in the long (90% of the time) glacial periods back in time…
When I wrote that (at WUWT), in next lectures that was not repeated anymore…
Next message for the other items…
LikeLike
The Salby lecture in 2014 has the most detail. He discusses and explains in his text books, not in blogs. There is far more information in his texts than could ever be put into blog posts.
CO2 migrates in liquid water, which is in, over and under ice. Ice in nature is rarely perfectly crystalline solid. Further, liquid water beneath ice is not in contact and exchanging with the atmosphere. When that interstitial water freezes, CO2 concentration in it would not be representative of atmospheric CO2 concentration there, much less anywhere else on the planet. Furthermore, it makes no sense to use ancient ice records for proxy CO2 calculations until you first explain and and have a validated model of present MEASURED CO2 conditions.
LikeLike
When I said to Ferdie that it seems like old times I was being literal: all of his arguments were addressed at Jo Nova in this Herculean thread which addressed this vital issue of whether human CO2, ACO2, is responsible for all or most of the undisputed increase in atmospheric CO2 over the last 150 years:
https://joannenova.com.au/2011/08/blockbuster-planetary-temperature-controls-co2-levels-not-humans/
After this thread Bob C did a considered proof showing ACO2 could not be responsible for all or most of the increase in CO2 which I’ll put up in my next post.
LikeLiked by 1 person
Some variables don’t need all the details of the world…
Take the increase in the atmosphere.
We know human emissions with reasonable accuracy: nowadays around 9 GtC/year. Accuracy +/- 0.5 GtC, probably more underestimated than overestimated by some countries (China…)
We know the increase in the atmosphere with reasonable accuracy: around 4.5 +/- 0.4 GtC/year.
We don’t know every single natural ins and outs to any accuracy, but we have some rough ideas about the main fluxes, based on δ13C and O2 measurements.
Is that a problem? Not at all. All we need to know for the mass balance is the two known variables: human emissions and increase in the atmosphere.
increase in the atmosphere = human emissions + natural sources – natural sinks
4.5 GtC/year = 9 GtC/year + X – Y
X – Y = -4.5 GtC/year.
Does it matter what X and Y exactly are? Not at all:
If X = 10 GtC/year then Y = 14.5 GtC/year
If X = 100 GtC/year then Y = 104.5 GtC/year
If X = 1000 GtC/year the Y = 1004.5 GtC/year
Thus without knowledge of any individual natural CO2 flux or the sum of all inputs or outputs, we know that nature is a net sink for CO2. It is really that simple…
The same for the CO2 uptake by the ocean surface layer:
Do you need all the equilibrium constants which change by temperature, salinity, etc.?
Not at all. Simply measure the net result over time of the increase in DIC by several fixed stations and compare that to the increase in the atmosphere which gives you an increase of DIC at about 10% of the increase in the atmosphere.
That is called the Revelle/buffer factor. Still 10 times higher in solubility for CO2 in seawater than for fresh water, but in both cases the increase in pure, dissolved CO2 is 100% of the increase in the atmosphere per Henry’s law.
Where then is the difference?
In fresh water pure CO2 is 99%, bicarbonate 1%, 0% carbonate. Thus a CO2 doubling doubles near all inorganic carbon forms in fresh water.
In seawater pure CO2 is 1%, bicarbonates 90% and carbonates 9%. If you double CO2 in the atmosphere then pure CO2 gets 2% and the rest increases a lot, but not 100%, as also H+ increases and pushes the equilibrium back to pure CO2…
See: https://tos.org/oceanography/assets/docs/27-1_bates.pdf Figure 3 and Table 2.
And the Bjerrum plot:
https://en.wikipedia.org/wiki/Bjerrum_plot
LikeLike
Ferdinand, sorry, but neither you nor anyone else knows human emission or even fossil fuel emission. That is an estimate only and based on highly suspect data. Fossil fuel emission is too small to be detected as a change in slope of net global average CO2. Yet we can easily measure the change in biological CO2 on daily, weekly, monthly and annual time scales.
LikeLike
Ferdinand, using your numbers as an example (but not agreeing with them.) Let’s say human emission is 4.5 GtC/year. Since 1 ppm CO2 = 2.12 GtC then 4.5 GtC per year = 2.1226 ppm CO2 emission per year. Then 2.1226 ppm CO2 emission divided by 415 ppm net global CO2 concentration = 0.5114% CO2 human emission as a % of net CO2 emission. But this omits that human CO2 emission is also absorbed in the environment. The 4.5 GtC/year is human emission not net human emission.
Human emission is a perturbation to the Henry’ Law phase state equilibrium equation. As Cohenite correctly points out, the perturbation is very quickly returned to the equilibrium condition. In other words, half of this 0.5114% is absorbed into the environment. See this short video https://archive.org/details/ucberkeley_webcast_sFbI9fAOsKE
If we look at the MLO CO2 concentration, with each year we can easily see a saw tooth increase in slope that peaks and then changes sign and rapidly decreases; these slope changes represent an increase in net emission and a more rapid decrease in net emission, then a return to the net emission ongoing multi-decade equilibrium trend. I am sure you have seen this NOAA MLO graph many times. So, for example the year centered on 2019, CO2 concentration increases from a minimum of 406 ppm to a maximum of 415 ppm and then back down to 409 ppm. We have a within year cyclical perturbation of positive 9 ppm then negative 6 ppm. We can safely assume that that the system can easily absorb half of the 2.1226 ppm emission since the system is cyclically emitting and absorbing more than double that amount. We can safely infer that net human emission is about 1.0613 ppm per year.
The slope of net global average CO2 concentration is increasing at about 2.58 ppm per year (MLO 2020 mean 414.24 minus 2019 mean 411.66 = 2.58 ppm). No matter how you may calculate it, human emission 2.1226 ppm/yr or net human emission 1.0613 pp/yr, the rate of change of human emissions is less than the rate of change of total emission 2.58 ppm/yr. The slopes are diverging. From this we safely deduce that human emission rate is not driving total emission rate.
Since CO2 is cumulative, a more correct comparison is the integral of the net global CO2 emission compared to the integral of the net human emission. This makes the dominance of net natural emission obvious. The graphic in my most recent blog posts attempts to show that comparison.
Another way to look at it: we have a mean 2.58 ppm per yr CO2 slope in the background signal with a variation as high as 9 ppm per year. But we only have a slope of 1.0613 ppm per year or 2.1226 ppm per year in the human CO2 signal. The slope of the human signal is 50% less than slope of the background signal and 8 times less than the variance in the slope of the background. In other words, the human signal cannot be distinguished from random noise in the background. For analytical precision and accuracy, signal needs to be at least 3 standard deviations larger than larger than the background noise in order to have 99% confidence level in the data, unless you have sophisticated signal processing capable of extracting signal from high background and noise.
LikeLike
Dear Bud,
Sorry for the delay in reply, my wife is quite ill (not from Covid, but some other lung disease) and hospitalized yesterday, so that took some time, but as no visit is allowed, due to Covid, we now have more time to respond…
I am a little confused by your answer, but let’s see what got right and wrong.
Human emissions are 9 GtC per year, not including land use change, or about 4.5 ppmv/year. No need to go into any accuracy, just rough estimates is all one needs.
I don’t know why you insist that this figure is not right, as that is based on sales (taxes) and certainly not overestimated. But let’s start with the 4.5 ppmv/year:
That is NOT a part of the total CO2 level that gives the net increase or decrease of CO2 in the atmosphere. The only part that influences the equilibrium is the amount above (or below) the equilibrium. The current (temperature dictated) equilibrium is around 295 ppmv and the only part that influences the equilibrium is 415 – 295 = 120 ppmv, as that is the driving force that drives CO2 from the atmosphere into the ocean surface, as 295 ppmv is what the current average pCO2 level of the ocean surface should be for the current average ocean surface temperature.
So we have a 120 ppmv disturbance in the atmosphere of a dynamic equilibrium process between atmosphere and ocean surface. How much CO2 does that push from the atmosphere into the ocean surface (and plant alveolars water) ?
If we may assume that the 4.5 ppmv human emissions are right and the increase in the atmosphere was measured as 2.25 ppmv in the same year, the net uptake by oceans and biosphere was 2.25 ppmv in the current year.
Be aware that the net uptake hardly depends of human emissions of one year: it only depends of the height of the current disturbance, which is 120 ppmv, not 4.5 ppmv.
If human emissions were zero, the net uptake by oceans and biosphere still would remain 2.25 ppm in the first year that human emissions stopped.
The next year a little less, as the disturbance dropped to 117.75 ppmv, etc,… until the old equilibrium is reached again…
There is a nice formula to give the decay rate for any disturbance of any process that gives a linear response (like in this case: the net sink rate is in linear ratio to the extra CO2):
Tau = disturbance / effect
Where Tau is the time needed to bring the disturbance down to 1/e or about 37% of the original disturbance.
Tau = 120 ppmv / 2.25 ppmv/year = 53 years
That thus is the problem: The increase in mass caused by human emissions (or volcanoes, or,…) is not removed in the same year as emitted, only half the mass is removed and that is why CO2 in the atmosphere -temporarily- keeps increasing…
If we could halve the emissions, then there would be no increase anymore. Which would be far less expensive than trying to get zero emissions (even if both are not necessary at all)…
The seasonal change of +/- 4.5 ppmv has nothing to do with the above: seasonal changes are driven by temperature, not by pressure.
What happens in spring/summer is about 51 GtC release by the warming ocean surface and at the same time a 60 GtC uptake by vegetation from growing new leaves and wood.
The opposite happens in fall/winter.
Net difference: +/-9 GtC or +/- 4.5 ppmv.
Net effect over a year: zero without disturbance, a cycle doesn’t change the mass balance when in equilibrium…
Net effect with 120 ppmv disturbance: -2.25 ppmv.
And as net human emissions are twice the increase in the atmosphere (*) humans are fully responsible for the CO2 increase…
As that is true for about every year in the past 60+ years, the accumulated emissions also are responsible for the accumulation in the atmosphere at twice their rate…
(*) Even with human emissions at 10% of the current atmosphere (measured as the drop in the 13C ratio) that gives that 10% of the current sinks are from the original human emissions, as the sinks don’t discriminate between human and natural CO2.
With a net sink rate of 2.25 ppmv/year the part in the sinks coming from humans is not more than 0.23 ppmv or the net contribution of humans still is 4.27 ppmv/year.
LikeLike
Ferdi, I am sorry your wife is ill. I hope she recovers quickly and completely.
You are really very confused about this Ferdi.
You cannot equate CO2 emission with net global average CO2 concentration. Net global average CO2 concentration is reported by NOAA Mauna Loa (MLO). It is total emission minus total absorption by all sources and sinks. Oak Ridge National Laboratories (ORNL) reports CO2 emission, not net emission, not emission minus absorption.
If the rate of change of net global average CO2 concentration was 2.25 ppmv per year, that rate of change is the net residual (the difference between absorption and emission) by all sources and sinks. All sources and sinks includes the very large annual cyclical rate of change (positive and negative slopes) due to photosynthesis differences between northern and southern hemispheres This is an annual disturbance to equilibrium which rebalances within each year.
The ORNL human CO2 emission for 2014 was 9855 million metric tons (Mmt) carbon which is a 4.65 ppmv CO2 disturbance to equilibrium. But that is only emission. That emission is offset by the same amount of CO2 absorption. According to Le Chatelier’s principle, the disturbance to the equilibrium is offset by an amount that returns the system to equilibrium. There is a 4.65 ppmv absorption that offsets the 4.65 ppm human emission. Net human emission is zero.
The disturbance to equilibrium caused by human emission works the same as the disturbance to equilibrium caused by photosynthesis, except the two cycles are out of phase.
The amount of human emission is statistically insignificant to the net global average CO2 concentration. The correlation between the rate of change of the net global average CO2 concentration and the rate of change of human emission is negative. These two points will now be shown:
In 2014 ORNL reported 9855 Mmt carbon emitted is 4.65 ppmv CO2
In 2013 ORNL reported 9773 Mmt carbon emitted is 4.61 ppmv CO2.
9.855 gigatonnes human carbon emission minus 9.773 gigatonnes human carbon emission = 0.082 gigatonnes increase in human carbon emission for the year 2013 to 2014 per ORNL. Ref: https://cdiac.ess-dive.lbl.gov/ftp/ndp030/global.1751_2014.ems
2.12 gigatonnes carbon = 1 PPM CO2 ( ref: IPCC and Gilbert Masters)
0.082 gigatonnes carbon divided by 2.12 gigatonnes C per ppmv CO2 = 0.037 ppmv per year CO2 human emission (only emission!, not emission minus absorption.)
In the same year period 2013 to 2014, NOAA Mauna Loa reported net CO2 for 2013 = 396.74 and 2014 = 398.87.
398.87 ppmv minus 396.76 ppmv equals 2.13 ppmv. The rate of increase in net global average CO2 concentration was 2.13 ppmv per year.
The rate of increase in human emission (only) was 0.037 ppmv, the rate of global net global average concentration (i.e. emission minus absorption) was 2.13 ppmv.
Then 2.13 divided by 0.037 = 57. In other words, net global average CO2 concentration (i.e. emission minus absorption) increased 57 times faster than human emission only! And we have not yet subtracted the amount of human CO2 that was absorbed in the same period. The 2.13 ppmv per year is the rate of annual of increase in net global average CO2 concentration. That rate is 57 times larger than the rate of increase in human emission only, and that number is significant understated because it does not include any absorption of human CO2 emission by the environment.
Obviously, the 57 times slower rate cannot be forcing or causing the rate of the 100 times larger cumulative CO2 concentration.
We do not know the total amount of CO2 emission from all sources nor do we know the total amount of CO2 absorption by all sinks. Such numbers are only estimates. We only know the net difference between total emission and total absorption, and MLO reports this amount and is the generally accepted proxy for net global average CO2 concentration.
The two trends or slopes (1) human emission and (2) cumulative concentration are diverging strongly. For a cause-and-effect relationship to exist, then there must be a positive correlation between the cause and effect. If there is no positive correlation, then a cause-effect relationship does not exist. Since the two trends (1) and (2) are diverging, there is no positive correlation. In other words, human emission is not causing the increase in net global CO2 concentration. Please read Professor Munshi’s paper at the link. He is an emeritus professor of statistics. “Responsiveness of atmospheric CO2 to fossil fuel emissions: Updated”. SSRN; 2017. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2997420
LikeLike
About CO2 in ice cores:
Ice cores are formed from snow and only at the ice-air surface there is some liquid-like layer of unordered water molecules where CO2 could “hide”.
Below -32°C that semi-liquid layer is absent. Moreover, if you push two ice spheres together, the liquid layer reorders and disappears to form non-liquid bridges together (or you can’t make snowballs… which is problematic if the snow is too cold…).
Thus while snow is compacting by the weight of new layers, that still has lots of open pores which get narrower with depth, but still are connected with the atmosphere. At 70-90 meter depth the pores are too narrow and then the remaining pores form isolated bubbles still complete air with all the CO2 in ratio to the (asymmetric) average atmosphere over the years that the bubbles needed to close.
Thus no “model” needed. Just measure any part that you want: CO2, O2/N2, CH4, N2O, freons,…
Migration was -theoretically- measured in the relative “warm” (-23°C) Siple Dome ice core on a melt layer. The result: a 10% broadening of the resolution from 20 to 22 years at middle depth and a doubling from 20 to 40 years at full depth. That is all.
For the much colder (-40°C) inland ice cores like Dome C and Vostok, migration is simply unmeasurably small.
Ice cores are not proxy’s. They contain old air with all the parts of the past available. Where there are clathrates present and below where there are no bubbles left under the high pressure, one starts with at least one year relaxation under cold conditions to restore the original volume. If that is not sufficient, total sublimation is preferred and mass spectrometry, so nothing van hide anywhere in the ice…
LikeLike
Bud, never heard of fossil fuel sales and all the taxes that the government earns from these sales? The government does like to collect all these taxes on coal, oil and gas sales, thus is very eager to know what is sold…
Thus is is easy to know what is sold and one does know the CO2 release by every type of fossil fuel. That is a straight forward calculation…
Maybe underestimated by under-the-counter sales to avoid taxes, but surely not overestimated…
LikeLike
Hi Ferdinand; just like the old days. CO2 increase is mainly natural:
https://www.sciencedirect.com/science/article/abs/pii/S0921818116304787
https://www.sciencepublishinggroup.com/journal/paperinfo?journalid=298&doi=10.11648/j.ijaos.20190301.13
https://www.researchgate.net/publication/257343053_The_phase_relation_between_atmospheric_carbon_dioxide_and_global_temperature
LikeLiked by 1 person
Dear Bud,
I tried to post a response to Cohenite but even with my Facebook account, that was not accepted.
So, I made a word file with the text, here attached…
A similar discussion was lately on WUWT as result of the publication of Dr. Ed Berry’s work, who made the same errors as many before him: https://wattsupwiththat.com/2021/12/25/physicist-dr-ed-berry-rips-un-ipccs-climate-fiction-explains-why-the-ipcc-is-wrong/
Best wishes for the new year!
Ferdinand
LikeLike
Ferdinand, your reply to Cohenite probably did not appear here because I took some time off for the holidays and did not get around to approving comments on my blog. Sorry. This does not imply that I agree with your comment.
LikeLike
Thanks for reading and responding Cohenite.
LikeLike
Dear Bud,
A few remarks about this work…
From the 420,000 years Vostok ice core, the ratio between temperature change and subsequent CO2 changes are about 8 ppmv/K over glacial and interglacial periods.
As the temperature of ice cores reflect mainly Antarctic temperatures where the snow was formed high in the atmosphere, the global change may be around 16 ppmv/K.
That includes all possible equilibria between oceans (deep and surface), land and ice sheet formation over thousands of years.
The 16 ppmv/K is also the main shift in solubility of CO2 in seawater for temperature changes around current average, Henry’s law and all subsequent equilibrium reactions included.
That means that for about 0.8 K average ocean surface temperature increase since the Little Ice Age there is about 13 ppmv CO2 increase caused by the change in solubility of CO2 in the ocean surface waters. All the rest of the 125 ppmv increase since the start of the industrial revolution is from the about 200 ppmv in total human emissions since 1850…
See further:
http://www.ferdinand-engelbeen.be/klimaat/co2_origin.html
In summary:
There is a good, one-way correlation with a lag of CO2 after temperature changes over short term (seasonal, inter annual) and very long term (glacial, interglacial), but the current increase of 125 ppmv above pre-industrial levels in 170 years time is far beyond the temperature increase and caused by human emissions.
If that has much influence on temperature, that is the question, which still has no clear answer. Anyway likely more beneficial than not and certainly not catastrophic…
LikeLike
Pingback: This fits the Henry’s Law theory | budbromley